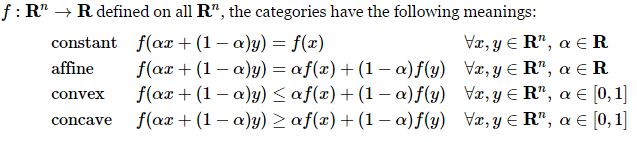The DCP Ruleset
1. 函数的分类
- 常量
- 仿射
- 凸
- 凹
定义:
这几个分类是有重叠的:比如常量属于仿射,仿射既属于凸也属于凹。
2. 最主要的规则
CVX支持以下3种DCP
- 最小化问题
- 目标函数为凸
- 约束条件可以有任意个
-
最大化问题 1. 目标函数为凹 2. 约束条件可以有任意个
- 可行性问题 1. 没有目标函数 2. 有1个或以上的约束条件
3. 约束条件
CVX支持以下3种约束条件
-
$=$ : 两侧都必须是仿射
-
$\preceq$:左侧为凸,右侧为凹
-
$\succeq$:左侧为凹,右侧为凸
3.1 具体要求
-
不支持
!=或者~= - 复数
- 等式约束的两侧可以是复数,可以分解为2个实数的约束。
- 不等式约束的两侧不能有复数
-
集合元素:集合元素的约束必须是等式,且等式两侧必须为仿射
- 严格不等(strict inequalities)
- $\prec$
- $\succ$
因为一些数学原理和凸优化算法的原因,CVX不能保证不等式被严格遵守,因此应该尽量不使用严格不等。
如果模型中必须用到严格不等,可以使用以下方法 消除严格不等 :
-
采用 正规化 的方法来使其符合CVX的要求。
例如:
可以转化为
-
添加一个 偏差(offset) 将原式变为非严格不等。
例如:
4. 表达式规则
-
常量表达式: 可以产生有限结果的表达式
- 仿射表达式:
- 常量表达式
- 已声明的变量
- 可产生有限结果的函数调用
- 仿射表达式的加减组合
- 常量和仿射表达式的乘积
- 凸表达式
- 常量或者仿射表达式
- 可产生凸结果的函数调用
- 仿射标量的偶数次方(不包括0次方)
- 2次凸标量
- 多个凸表达式的和
- 凸表达式和凹表达式的差
- 非负常量和凸表达式的乘积
- 非正常量和凹表达式的乘积
- 凹表达式取反
- 凹表达式
- 常量或者仿射表达式
- 可产生凹结果的函数调用
- 凹标量的$p$次方($0< p < 1$)
- 2次凹标量
- 多个凹表达式的和
- 凹表达式和凸表达式的差
- 非负常量和凹表达式的乘积
- 非正常量和凸表达式的乘积
- 凸表达式取反
-
任何不符合以上规则的表达式都会被CVX禁止,尽管它可能是凸的。
-
涉及到矩阵时以其中的元素作为考量。
-
不支持非标量之间的乘法
例如:
x*sqrt{x}不被接受,但可以用pow_p(x, 3/2)替代。
5. 函数
CVX中的函数有2个特征:曲度(curvature)和单调性。
-
变量必须在函数的隐含定义域中。只需定义用户自定的定义域。 例如,不用为添加$x\ge0$的约束。
-
CVX判断凹凸时不考虑隐含的定义域或者自定的定义域,在定义域外为$+\inf$的被认为是凸,反之为凹。
例如:$\frac{1}{x} \quad s.t. x \ge 1$ 不被CVX认为是凸的,尽管它事实上是。解决方法是将$x < 0$ 的区域的函数值定义为$+\inf$,可以用CVX的函数
inv_pos(x)来完成。反之,-inv_pos(-x)将表示凹的版本。 -
CVX判断单调性时不考虑定义域,比如$\sqrt{x}$在$x < 0$的区域任然被认为是非减的。
-
多元函数的凹凸性是由所有变量联合决定的,但单调性可以按每个变量来讨论。
-
有些多元函数仅对一部分参数是凸的,凹的,仿射的,此时其他参数必须设为常数。比如:
仅仅对$x$是凸的,因此在CVX中$p$必须设为常数。
-
函数嵌套:
凸函数、凹函数、仿射函数可以接受一个仿射表达式,结果相应为凸、凹、仿射的。
当已知 函数为凸 和函数对于各个参数的单调性时:
-
函数对于某参数不减:这个参数必须是凸的
-
函数对于某参数不增:这个参数必须是凹的
-
函数对于某参数不减不增:这个参数必须是仿射的
当每个参数都满足以上条件,这个函数就是凸的并且可以被CVX接受。函数为凹时第1,2条相反,第3条相同。
例如:
-
max(abs(x)),其中x时向量。max函数是凸的并且对于任一参数不减,并且abs函数也是凸的,因此整体是凸的。 -
sum(sqrt(x)),因为sum函数是仿射且不减的,而sqrt是凹的,因此整体为凹。同理sum(square(x))是凸的。
-
-
非线性嵌套的单调性
因为很多凸函数在定义域上没有单调性,因此不能直接使用(自行定义定义域也不行)。CVX的很多函数有2种形式,一种是原始的,一种是在固定定义域有单调性的。例如:
square_pos()sum_square_pos()quad_pos_over_lin() -
关于平方
事实上,CVX原本并不支持平方表达式,但CVX将自动识别以下几种边的表达式
- $x . * x$
- $conj( x ) . * x$
- $y’ * y$
- $(A * x - b)’ * Q * (Ax-b)$
并将其转为相应的可接受的形式:
sum_square_abs( y )sum_square_abs( y )sum_square_abs( y )quad_form( A * x - b, Q )
CVX建议尽量少用平方,因为平方是平滑的,它一般是作为非平滑的真实目标函数的替代,然而CVX本身支持很多的非平滑函数。因此使用非平方可以更加精确。例如: sum( ( A * x - b ) . ^ 2 ) <= 1 可以用 norm( A * x - b )<= 1 替代,也就是欧式范数。