Generative Adversarial Nets
Authors: Ian J. Goodfellow*, Jean Pouget-Abadie†, Mehdi Mirza, Bing Xu, DavidWarde-Farley,Sherjil Ozair‡, Aaron Courville, Yoshua Bengio§
1. Introduction
GANs启发自博弈论中的二人零和博弈,包含一个生成模型(generative model G)和一个判别模型(discriminative model D)。
生成模型捕捉样本数据的分布,判别模型是一个二分类器。
生成器G需要让D把自己产生的伪造图片全部判断成真实的图片,判别器 D 需要判断输入数据是真实的图片还是伪造的图片。
2. Related work
3. Adversarial nets
真实输入数据的分布:$p_x$
由$G$输出的数据的分布:$p_g$
输入随机噪声$z$的分布:$p_z(z)$
生成函数$G$:将随机噪声映射到数据空间:$G(z)$
判别函数$D$:判断输入数据来自数据空间还是生成器$G$空间(也就是判断输入是真实的数据还是G生成的数据),输出是一个概率值
优化目标:
-
最大化$D$的准确度$logD(x)$,使其尽可能将原始数据准确分类
-
最小化$log(1-D(G(z)))$,使其尽可能将生成数据准确分类
目标函数:
优化过程:
-
先完全优化$D(x)$将很耗时,并且再数据集有限的情况下会导致过拟合。因此先在优化$D$$k$次,再优化$G$1次,如此循环。
-
在训练的起始阶段,相比$D$来说,$G$很弱。因此$D$的置信度很高,导致$log(1-D(G(z)))$饱和。所以用最大化$log(D(G(z)))$来替代最小化$log(1-D(G(z)))$。这样可以为$G$提供更大的梯度使其成长。 (why?)
-
当$p_g=p_x$时,也就是$G$生成的图像与真实输入有相同的分布时,达到全局最优点,此时$D(x)=0.5$
4. Theoretical result
-
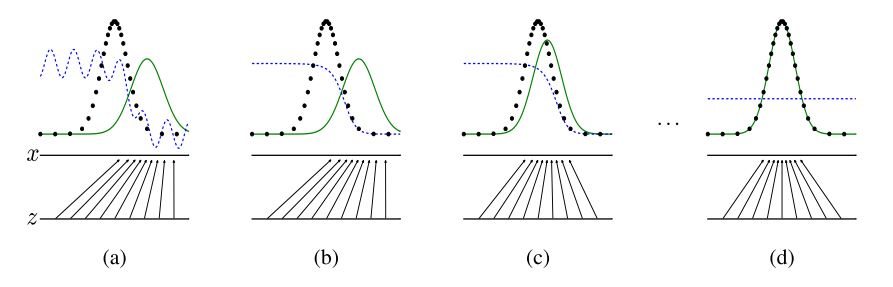
黑线:真实数据分布$p_x$
-
蓝线:$D$
-
绿线:$G$生成的数据的分布$p_g$
可以看见$G$生成的数据逐渐在向真实数据分布$p_x$靠近,而$D$试图尽可能区分二者。
算法伪代码如下:
5. Experiments
激活函数:
-
$G$: 同时使用了relu和sigmoid
-
$D$: maxout
Dropout和noise:
-
训练$D$的过程中使用了dropout
-
尽管理论上训练$G$的时候在任何层都可以用dropout和添加noise,但实际只在最底层在输入中添加了nosie。(why?)
6. Advantages and disadvantages
缺点:
- $G$和$D$的训练必须要保持同步
优点:
-
不需要使用Markov chains,只用反向传播就能获得梯度。
-
优化$G$的过程不直接使用样本,而是用样本的梯度来优化。避免了样本的内容被直接拷贝到生成网络的参数中。
-
可以表示很sharp和degenerate的分布。